359. Circle and line
There is a circle of
radius R with center at (x, y) and the line that is gi\ven with the
coordinates of its two points. Find the length of the line segment inside the
circle.
Input.
One line contains radius of the circle R, the coordinates (x, y) of the circle center and coordinates of two points on the line.
All numbers are integers, not greater than 10000 by absolute value.
Output. Print the length of the line segment inside the circle
with 5 digits after the decimal point. If the circle and the line do
not intersect, print -1, if touches – print 0.
|
Sample input |
Sample output |
|
5 0 0
4 1 4 2 |
6.00000 |
SOLUTION
geometry
Algorithm analysis
The equation of the line that pass
throug the points (x1,
y1) and (x2, y2) has the form
 ,
,
or after simplification
x (y2 – y1) + y (–x2 + x1) – x1
* y2 + y1 * x2 = 0
If the equation has the form ax + by + c
= 0, then
a = y2 – y1, b = –x2 + x1, c = – x1 * y2 + y1
* x2
The distance from the line ax + by
+ c = 0 to the center (x0, y0) of the circle equals
to
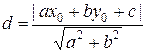
If d
> r then circle and line
do not intersect.
If d = r then circle and line touch each other.
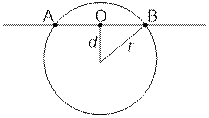
Consider the case d
< r and find the length of segment AB of a line in the circle: AB = 2
* OB = 2 ![]() .
.
Example
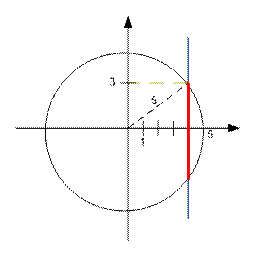
In the
given sample, a circle with radius 5 and center (0, 0) is given. A
straight line
has an equation x = 4. The length of the line’s part inside the circle is 6.
Algorithm realization
Read the input
data. The center of the circle has coordinates (xx0, yy0). The line passes through the points (xx1, yy1) and (xx2, yy2).
scanf("%d %d %d %d %d %d %d",&r,&xx0,&yy0,&xx1,&yy1,&xx2,&yy2);
Compute the
coefficients a, b and c of the line ax + by + c
= 0 that pass
through the points (xx1,
yy1) and (xx2, yy2).
a
= yy2 - yy1; b = -xx2 + xx1;
c
= -xx1*yy2 + yy1*xx2;
Compute
the distance d from the
center of a circle (xx0,
yy0) to the line ax + by + c
= 0.
d
= abs(a * xx0 + b * yy0 + c) / sqrt(1.0 * a * a + b* b);
If d
> r then circle and line
do not intersect.
if
(d > r) printf("-1\n"); else
If d = r then circle and line touch each other.
if
(d == r) printf("0\n");
else
{
Compute
and print the length of a line segment inside a circle.
res = 2 * sqrt(1.0 * r * r - d * d);
printf("%.5lf\n",res);
}
Java
realization
import java.util.*;
public class Main
{
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
double r = con.nextDouble();
double x0 = con.nextDouble();
double y0 = con.nextDouble();
double x1 = con.nextDouble();
double y1 = con.nextDouble();
double x2 = con.nextDouble();
double y2 = con.nextDouble();
double a = y2 - y1;
double b = -x2 + x1;
double c = -x1 * y2 + y1 * x2; // ax + by +
c = 0
double d = Math.abs(a * x0 + b * y0 + c) / Math.sqrt(a * a + b * b);
if (d > r) System.out.println(-1); else
if (d == r) System.out.println(0); else
{
double res = 2 * Math.sqrt(r * r - d * d);
System.out.println(res);
}
con.close();
}
}